[다익스트라 알고리즘]LeetCode 743.네트워크 딜레이 타임 | Python
LeetCode - The World's Leading Online Programming Learning Platform
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
1. 문제
k에서 출발해 모든 노드가 신호를 받을 수 있는 시간을 계산하라.
한 군데라도 노드에 도달할 수 없는 경우 -1을 리턴한다.
입력값(u,v,w)는 각각 출발지, 도착지, 소요 시간으로 구성되며, 전체 노드의 개수는 n이다.
제약조건
- 1 <= k <= n <= 100
- 1 <= times.length <= 6000
- times[i].length == 3
- 1 <= ui, vi <= n
- ui != vi
- 0 <= wi <= 100
- 모든 쌍은 고유 합니다 . (즉, 다중 모서리가 없습니다.)(ui, vi)
2. 풀이
1) 문제를 풀기 위해 알아야 할 개념
💡힙(Heap)
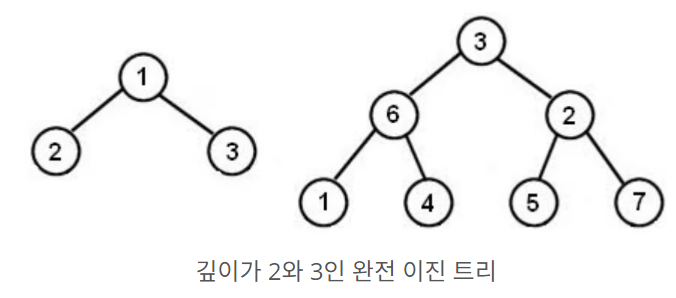
힙은 정렬 알고리즘과 같이 최솟값 또는 최댓값을 반복적으로 찾아야 하는 상황에서 효율적으로 사용할 수 있다.
이 문제에서 '모든 노드가 신호를 받는 데 걸리는 시간'을 찾아야한다.
이 말은 즉슨 가장 오래 걸리는 노드까지의 최단 시간을 말한다.
그래서 힙 자료구조를 쓰면 효율적이다.
💡우선순위 큐(Priprity Queue)
우선순위를 가진 요소들을 관리하는 추상적 자료구조다.
힙은 우선순위큐를 구현하는데에 적합한 자료구조다.
q는 힙구조로 튜플 (거리, 노드번호)를 원소로 갖고 heapq.heappop(q)를 사용하여 최단 거리를 가진 노드를 큐에서 꺼내온다.
q = [(0, start)]
distance[start] = 0
while q:
dist, now = heapq.heappop(q)
2) 코드
(※ 파이썬 문법을 공부할 겸 푼거라 주석이 많습니다.)
1️⃣ 최소힙 모듈(heapq)을 import해온다. (times를 입력받기 위해 json을 import해온다.)
2️⃣ 진입점이 되어줄 함수를 만들어준다. (network_delay_time)
- 네트워크 딜레이 타임을 계산하는 주요 로직을 포함한다.
- dijkstra 함수 : 최단거리를 저장하는 리스트인 'distance'를 업데이트함.
3️⃣ 힙을 이용하여 우선순위큐를 구현해준다.
4️⃣ 입출력 부분을 구현해준다.
<주석 있는 버전>
import heapq
import json
# network_delay_time 함수는 네트워크 딜레이 타임을 계산함.
# network_delay_time 함수는 전체 프로그램의 진입점.
def network_delay_time(times, N, K): #times: []로 구성되는 출발지 도착지 소요시간, n은 노드수, k는 출발지.
# N+1개의 빈배열을 만들어 graph에 할당한다. 인덱스 0을 사용하지 않으려고 +1을 해준다.
# 루프 내에서 변수를 사용하지 않을때 언더바(_)를 씀.
graph = [[] for _ in range(N + 1)]
# 주어진 간선 정보(times)를 순회한다. times는 리스트고 u,v,w는 변수다.
# graph의 각 인덱스가 하나의 노드를 대표함.'u'번째 요소에 (v,w)튜플을 추가함.
for u, v, w in times:
graph[u].append((v, w))
# 최단 경로를 저장할 리스트를 무한대 값으로 초기화한다.
# 코드 실행 전에는 모든 노드까지의 거리를 모르는 상태이기 때문에 '무한대'로 초기화해주는게 일반적이다.
# (N+1)을 곱해주는 것은 무한대로 초기화 한 배열을 N+1만큼 생성한다는 의미다.
distance = [float('inf')] * (N + 1)
# 다익스트라 알고리즘을 구현하는 내부 함수. 함수선언은 def로 함.
# dijkstra 함수는 network_delay_time 함수 내에서만 호출할 수 있다.
def dijkstra(start):
q = [(0, start)] # 시작 노드와 거리(0)를 튜플로 큐에 넣음.
distance[start] = 0 # 시작 노드의 최단 거리를 0으로 설정함.
while q: # 큐가 빌 때까지 반복합니다.
# 힙에서 거리가 가장 짧은 노드를 꺼냄.(heapq모듈이 최소힙을 구현!)
# 힙의 루트(힙의 첫번째요소)는 항상 힙 내에서 가장 작은 값.
# 'q'힙에는 (거리, 노드 번호)가 추가되어있고, '거리'값을 기준으로 정렬됨.
dist, now = heapq.heappop(q)
# 이미 더 짧은 경로를 통해 now에 도달했는지 확인하고자 조건문 씀.
if distance[now] < dist:
continue # 이미 처리된 노드는 패스함.
# 현재 노드와 인접한 노드들을 순회한다.
for v, w in graph[now]:
# 현재 노드를 거쳐 인접 노드로 가는 비용을 계산합니다.
cost = dist + w
# 계산된 비용이 기존의 최단 거리보다 작으면 업데이트함.
if cost < distance[v]:
distance[v] = cost
# 'q'힙에 (cost,v) 튜플을 추가한다.
heapq.heappush(q, (cost, v))
# 시작 노드 K에서 다익스트라 알고리즘을 실행
dijkstra(K)
# 모든 노드까지의 최대 딜레이 시간을 계산함.
#리스트[시작인덱스:끝인덱스] => distance[1:]은 리스트 두번째부터 마지막까지 선택한다는 뜻.
#왜? 0번 인덱스를 사용하지 않고 1번인덱스=1번노드이기 때문!
max_distance = max(distance[1:])
# 최대 딜레이 시간이 무한대가 아니면 해당 값을(노드에 도달하면), 그렇지 않으면 -1을 반환한다.
# 파이썬의 조건부 표현식 : X if 조건 else Y
# 조건이 참이면 x를 반환하고 아니면 Y를 반환한다.
return max_distance if max_distance < float('inf') else -1
##### 사용자 입력을 받는 부분 #####
#리스트 형식은 JSON형식으로 변환할 필요없음.
times = json.loads(input())
N = int(input()) # 노드의 개수를 입력받습니다.
K = int(input())
# 함수를 호출하여 결과를 계산하고 출력합니다.
delay_time = network_delay_time(times, N, K)
print(delay_time)
<주석 없는 버전>
import heapq
import json
def network_delay_time(times, N, K):
graph = [[] for _ in range(N + 1)]
for u, v, w in times:
graph[u].append((v, w))
distance = [float('inf')] * (N + 1)
def dijkstra(start):
q = [(0, start)]
distance[start] = 0
while q:
dist, now = heapq.heappop(q)
if distance[now] < dist:
continue
for v, w in graph[now]:
cost = dist + w
if cost < distance[v]:
distance[v] = cost
heapq.heappush(q, (cost, v))
dijkstra(K)
max_distance = max(distance[1:])
return max_distance if max_distance < float('inf') else -1
# 사용자 입력을 받는 부분
times = json.loads(input())
N = int(input())
K = int(input())
delay_time = network_delay_time(times, N, K)
print(delay_time)