코딩 테스트 문제 중에 프로그램 실행 시간이 특정 시간 미만이어야 한다는 조건이 있는 경우가 있습니다.
효율성을 측정하는 문제의 경우 대부분 입력 크기가 매우 큽니다.
우리가 작성하는 코드의 실행 시간이 입력 데이터의 크기와 어떤 상관관계가 있는지 파악해서 효율성을 계산해야합니다.
알고리즘의 실행 시간과 데이터의 상관관계를 시간 복잡도라고 합니다.
시간 복잡도는 코딩 테스트 준비를 본격적으로 시작하기 전에 꼭 알아야 할 개념 중 하나입니다.
1. 시간 복잡도란?
함수의 실행 시간을 표현하는 것.
주로 점근적 분석을 통해 실행 시간을 단순하게 표현합니다.
시간 복잡도는 빅오(Big-O) 표기법을 사용합니다.
2. 빅오 표기법
알고리즘이 겪을 수 있는 최악의 경우에 걸리는 시간과 입력 간의 상관관계를 표현하는 표기법입니다.
빅오 표기법의 원리에 대해 알아봅시다.
✔️코드 실행시간은 실행환경에 따라 다를 수 있기 때문에 시간 단위로 계산하는 것이 아닌 함수,알고리즘 수행에 필요한 스텝(step)수로 표현합니다.
✔️ 각 라인을 수행하기 위해 필요한 스텝 수는 상수(constant)라고 가정해봅니다.

c1,c4는 한 번만 실행될 겁니다.
c2의 times가 N+1인 이유는 for문을 다 돌고나서 for문을 탈출하기 위한 검사를 한번 더 하기 때문에 +1을 해주고요.
c3는 입력 데이터의 크기(N)만큼 실행됩니다.
✔️ 실행시간(N)을 계산해 봅니다.
= c1*1 + c2*(N+1) + c3*N + c4*1
= (c2 + c3)*N + c1+c2+c4
간단하게 표현하면
=> a*N + b 이 됩니다.
우리가 궁금한 것은 입력 데이터가 클 때의 실행 시간입니다.
때문에 점근적 분석법으로 실행시간을 계산합니다.
※점근적 분석법: N이 ∞무한대로 갈 때, 어떤 함수 형태에 근접해지는지 분석하는 것
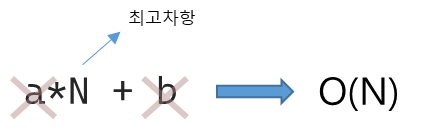
- N이 커질 수록 덜 중요한 것은 제거합니다.
- 최고차항만 의미가 있습니다.
- 최고차항의 계수는 의미가 없습니다.
boolean exists(int[] inputs, int target){
for(int i = 0; i < inputs.length; i++){
if(inputs[i] == target){
return true;
}
}
return false;
}
위 코드는 inputs 배열을 순회하며 target을 찾는 코드입니다.
best => target이 0번 인덱스에 있다면 실행시간은 1입니다.
최단 시간 실행을 O(1) 로 표현합니다.
worst => target이 마지막에 존재하거나 존재하지 않다면 배열의 크기만큼 실행시간이 걸릴겁니다.
최장 시간 실행을 O(N)으로 표현합니다.
빅오 표기법은 알고리즘이 겪을 수 있는 최악의 경우에 걸리는 시간과 입력 간의 상관관계를 표현하는 표기법이기때문에
위 코드의 시간 복잡도는 O(N)입니다.
3. 시간 복잡도 그래프
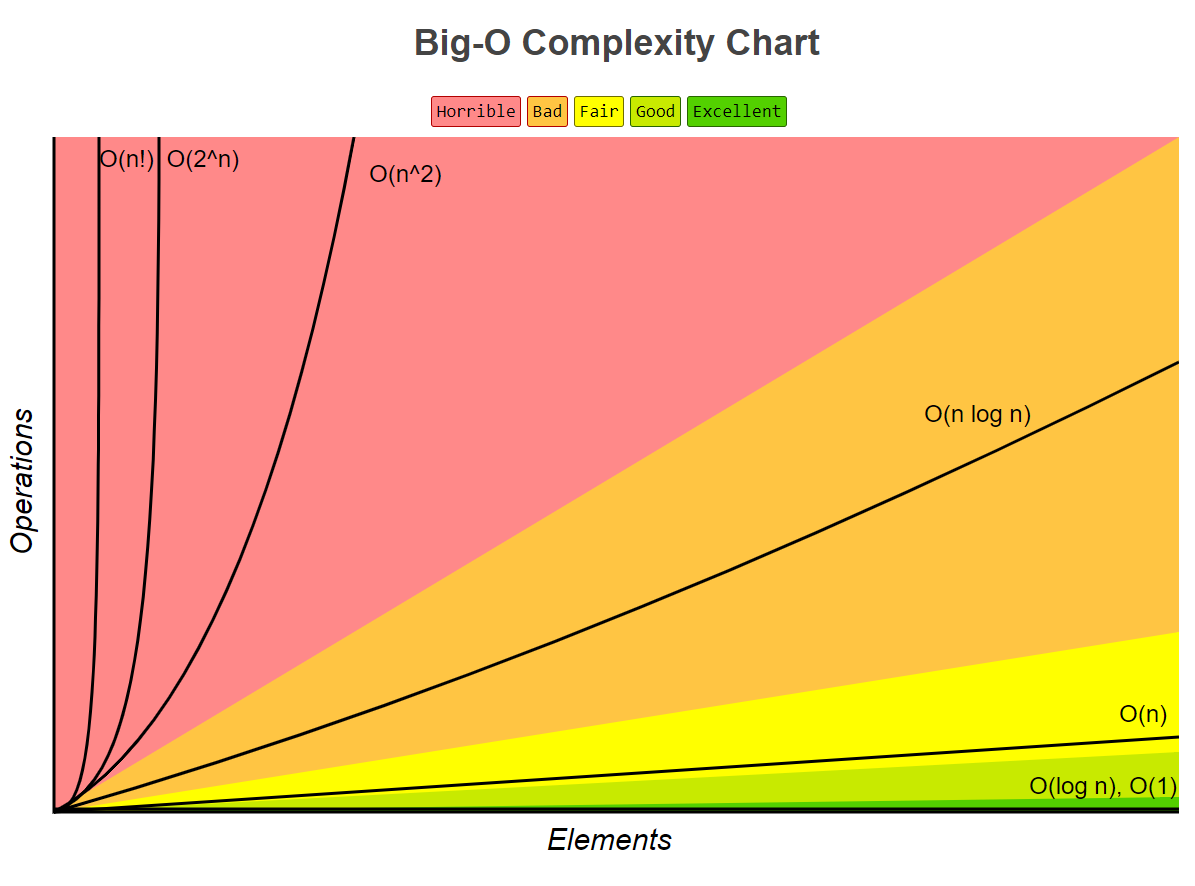
입력 데이터의 크기 (N)이 커질수록 시간 복잡도의 결과값 차이가 굉장히 커진다는 것을 그래프로 확인할 수 있습니다.
규모가 큰 서비스일수록 효율적인 코드가 중요합니다.
그래서 기업에서 코딩테스트 실력을 보는 것이고 코딩테스트 공부를 시작하기 전에 시간복잡도에 대해 알아야합니다.
4. 시간 복잡도 계산하기
시간 복잡도는 정확한 실행 시간을 계산하는 용도가 아닙니다.
점근적 분석법으로 상수 부분을 제외하고 표기합니다.
예를 들어, 길이가 N인 배열의 반만 사용하는 알고리즘은 빅오 표기법으로 O(N/2)으로 나타낼 수 있지만
상수 부분을 제외하고 O(N)으로 표기합니다.
길이가 N인 배열을 두 번 반복하는 경우 또한 O(2N)이 아니라 O(N)으로 표기합니다.
하지만, 길이가 N인 배열을 M번 반복한다면 시간 복잡도는 O(NM)이 됩니다.
또는 길이가 N인 배열을 순회하고나서 길이가 M인 배열을 순회한다면 시간 복잡도는 O(N+M)으로 표기합니다.
5. 시간 복잡도 줄이는 방법

오른쪽으로 갈수록 시간복잡도가 증가합니다.
(모바일로 보니 이미지가 쬐깐하게 나와서 텍스트도 추가합니다.)
O(1)->O(logN)->O(N)->O(NlogN)->O(N^2)->O(2^N)->O(N!)
✔️배열의 모든 원소를 순회한다면 O(N)의 시간 복잡도가 소요됩니다.
→ 배열이 정렬되어 있다면 이진 탐색을 적용하여 시간 복잡도는 O(logN)이 되므로 효율적으로 탐색할 수 있습니다.
✔️ 배열에서 중복을 제거한 원소를 찾고 싶을 때 원소별로 배열 전체를 순회하면 O(N²)의 시간 복잡도가 소요됩니다.
→ 자료 구조 Set을 이용하면 O(N)으로 해결할 수 있습니다.
따라서 문제 조건에 맞는 적절한 알고리즘과 자료구조를 이용하는 것이 핵심입니다.
6. 알고리즘 사용할 때 시간 복잡도 생각해보기
1) 이진탐색 알고리즘 O(logN)
public class BinarySearch {
public static int binarySearch(int[] arr, int target) {
int left = 0; // 탐색 범위의 왼쪽 인덱스
int right = arr.length - 1; // 탐색 범위의 오른쪽 인덱스
while (left <= right) {
int mid = left + (right - left) / 2; // 탐색 범위의 중간 인덱스
if (arr[mid] == target) {
return mid; // 원하는 값이 중간 값과 일치하면 해당 인덱스를 반환
} else if (arr[mid] < target) {
left = mid + 1; // 중간 값보다 크면 오른쪽 반을 탐색
} else {
right = mid - 1; // 중간 값보다 작으면 왼쪽 반을 탐색
}
}
return -1; // 원하는 값이 배열에 없을 경우 -1을 반환
}
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
int target = 6;
int result = binarySearch(arr, target);
if (result != -1) {
System.out.println("찾고자 하는 값 " + target + "은(는) 배열의 인덱스 " + result + "에 위치합니다.");
} else {
System.out.println("찾고자 하는 값 " + target + "은(는) 배열에 없습니다.");
}
}
}
매번 실행할 때마다 ½씩 사이즈가 줄어듭니다.
몇 번만에 사이즈가 1이 되는지 구해야합니다.
입력 데이터 크기는 N이라고 했을 때,
N*(1/2)^k = 1 로 식을 세워볼 수 있습니다.
k를 구하면 시간 복잡도를 알 수 있습니다.
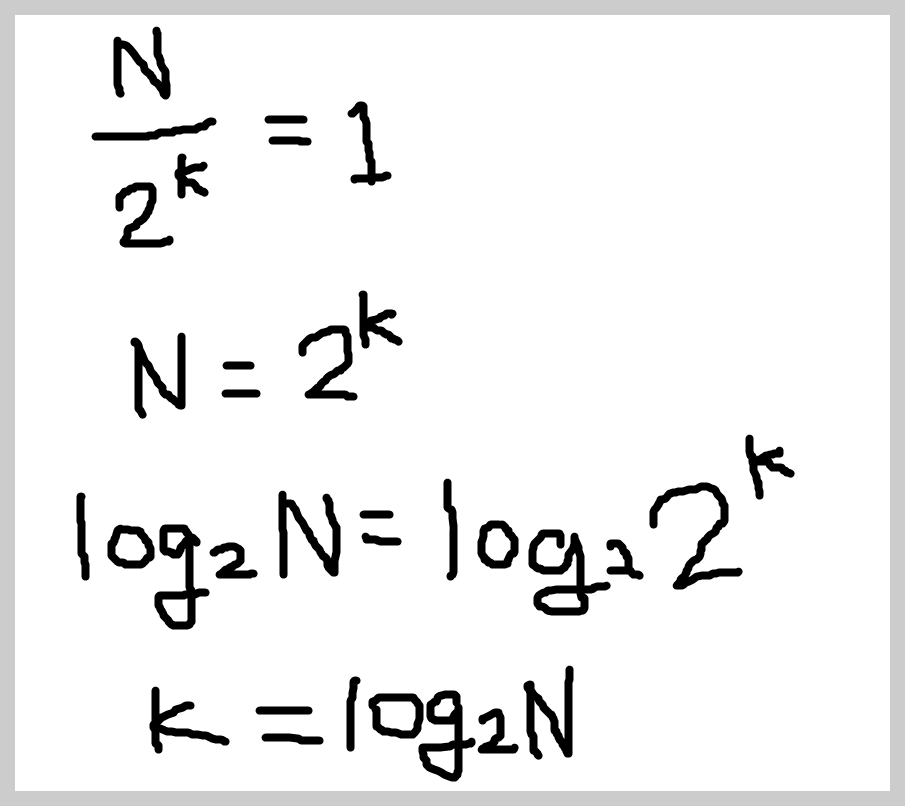
이것을 빅오 표기법으로 표기하면 O(logN)이 됩니다.
2) 병합 정렬 알고리즘 O(NlogN)
import java.util.Arrays;
public class MergeSort {
// 배열을 정렬하는 메서드
public static void mergeSort(int[] arr) {
// 배열의 크기가 1 이하면 이미 정렬된 상태이므로 종료
if (arr.length <= 1) {
return;
}
// 배열을 중간 지점을 기준으로 왼쪽과 오른쪽으로 나눔
int middle = arr.length / 2;
int[] left = new int[middle];
int[] right = new int[arr.length - middle];
for (int i = 0; i < middle; i++) {
left[i] = arr[i];
}
for (int i = middle; i < arr.length; i++) {
right[i - middle] = arr[i];
}
// 왼쪽과 오른쪽 부분 배열을 재귀적으로 정렬
mergeSort(left);
mergeSort(right);
// 정렬된 왼쪽과 오른쪽 부분 배열을 병합
merge(arr, left, right);
}
// 두 개의 정렬된 배열을 병합하는 메서드
public static void merge(int[] arr, int[] left, int[] right) {
int i = 0, j = 0, k = 0;
while (i < left.length && j < right.length) {
// 왼쪽과 오른쪽 배열을 비교하여 작은 값을 원래 배열에 병합
if (left[i] <= right[j]) {
arr[k++] = left[i++];
} else {
arr[k++] = right[j++];
}
}
// 남은 요소들을 병합
while (i < left.length) {
arr[k++] = left[i++];
}
while (j < right.length) {
arr[k++] = right[j++];
}
}
public static void main(String[] args) {
int[] arr = {12, 11, 13, 5, 6, 7};
System.out.println("정렬 전 배열: " + Arrays.toString(arr));
mergeSort(arr);
System.out.println("정렬 후 배열: " + Arrays.toString(arr));
}
}시간 복잡도가 O(NlogN)인 이유는 각 단계마다 데이터를 반으로 나누는 분할(Divide) 단계와 이후에 병합(Conquer)하는 단계가 모든 데이터에 대해 logN 단계 수행되고, 각 단계에서 N번의 연산이 수행되기 때문입니다.
3) 버블 정렬 알고리즘 O(N²)
일반적으로 이중 반복문을 사용하는 알고리즘은 시간복잡도가 O(N²) 입니다.
이러한 알고리즘은 각 요소에 대해 다른 모든 요소를 한 번씩 확인해야 하므로, 입력 크기 N에 대해 N² 번의 연산을 수행합니다.
public class BubbleSort {
// 버블 정렬 메소드
public static void bubbleSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) { // 외부 루프: 전체 배열을 순회
for (int j = 0; j < n - i - 1; j++) { // 내부 루프: 정렬되지 않은 부분을 순회
// 인접한 요소를 비교하고 필요한 경우 위치 교환
if (arr[j] > arr[j + 1]) {
// 요소 교환
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
}
4) 재귀적으로 구현한 O(2^N) 피보나치 수열을 동적프로그래밍을 사용하여 O(N)의 시간복잡도로 개선하기
시간복잡도가 O(2^N)인 알고리즘은 대개 재귀적 구조를 가지고 있으며 각 단계에서 두 개의 분기로 나뉘어 처리량이 기하급수적으로 증가합니다.
O(2^N)의 시간복잡도를 가지는 알고리즘 코드는 입력 데이터(N)가 클수록 비효율적인 알고리즘이기때문에 효율적으로 개선해줘야합니다.
✔️ 재귀적으로 구현한 피보나치 수열 O(2^N)
public class Fibonacci {
// 피보나치 수열을 계산하는 재귀 메소드
public static int fibonacci(int n) {
if (n <= 1) {
return n;
}
return fibonacci(n - 1) + fibonacci(n - 2); //함수내에서 자기자신을 호출(재귀)
}
public static void main(String[] args) {
int n = 10; // 예시로 10번째 피보나치 수를 계산
System.out.println("피보나치 수열의 10번째 수: " + fibonacci(n));
}
}
//트리형태로 나타낸 재귀호출 구조
fibonacci(n)
├─ fibonacci(n-1)
│ ├─ fibonacci(n-2)
│ └─ fibonacci(n-3)
└─ fibonacci(n-2)
├─ fibonacci(n-3)
└─ fibonacci(n-4)
각 단계에서 호출 횟수가 두 배씩 증가합니다.
첫 번째 단계에서는 1회, 두 번째 단계에서는 2회, 세 번째 단계에서는 4회의 호출이 발생합니다.
이러한 패턴은 n번째 단계까지 계속되며, n번째 단계에서는 대략 2^n회의 호출이 발생합니다.
✔️ 동적 프로그래밍을 이용한 피보나치 수열 O(N)
public class FibonacciDP {
// 피보나치 수열을 계산하는 동적 프로그래밍 메소드
public static int fibonacciDP(int n) {
if (n <= 1) {
return n;
}
int[] fib = new int[n + 1];
fib[0] = 0;// 피보나치 수열의 첫 번째 숫자 초기화
fib[1] = 1;// 피보나치 수열의 두 번째 숫자 초기화
for (int i = 2; i <= n; i++) {
fib[i] = fib[i - 1] + fib[i - 2];// i번째 피보나치 수 계산 및 저장
}
return fib[n];
}
public static void main(String[] args) {
int n = 10; // 예시로 10번째 피보나치 수를 계산
System.out.println("피보나치 수열의 10번째 수: " + fibonacciDP(n));
}
}동적 프로그래밍을 이용하여 피보나치 수열을 구현했을 때, 시간 복잡도가 O(N)이 되는 이유는
각 숫자를 한 번만 계산하고, 그 결과를 저장하여 재사용하기 때문입니다.
이 방법은 중복 계산을 방지하고, 각 숫자를 계산하는 데 필요한 시간을 최소화합니다.
총 연산 횟수는 입력 크기 N에 직접 비례합니다.
따라서, 시간 복잡도는 O(N)이 됩니다.
이는 재귀적 방법의 O(2^N)에 비해 훨씬 효율적입니다.
7. 오늘의 회고
어제 모른건 오늘 알면 된다.

오전엔 수업듣고 오후에 팀플젝하고 집와서 블로그포스팅하니까 기분이 매우 좋다.
벽처럼 느껴졌던 시간 복잡도, 빅오 표기법..이제야 좀 알것 같다.
1월의 나는 알고리즘 바보지만 5개월 뒤의 나는 알고리즘 고수가 되어있을 거당.
얍 다 뿌셔.
[출처]
문제집 - 프로그래머스 코딩테스트 문제 풀이 전략 : 자바편
유튜브 - https://youtu.be/tTFoClBZutw?si=AZO3h4_iSDQdwtJk
'알고리즘&자료구조 > Algorithm' 카테고리의 다른 글
| [백트래킹] LeetCode 17. 전화번호 문자 조합 (1) | 2024.01.15 |
|---|---|
| [DFS]LeetCode 200번. 섬의 개수 (1) | 2024.01.11 |
| 대소문자 변환 (1) | 2023.12.17 |
| 문자찾기 (1) | 2023.12.17 |
| [알고리즘]백준 2644번 촌수계산(DFS와 BFS알고리즘) (1) | 2023.10.21 |
